多軸運動系統誤差預算分析

精密定位的系統級誤差評估與最小化策略

作者：John Lindell 應用工程經理

本文將闡述如何分析多軸運動系統，以估算其功能點（或稱工作點）的誤差，內容將深入探討如何檢視系統幾何結構，以及如何將元件級誤差轉換為系統級誤差的具體細節，同時，文中也將檢視一種建議的計算方法，並探討改善系統性能的途徑。

為何多軸誤差至關重要？

現代製造流程正產生日益複雜的零件幾何形狀與持續縮小的公差，諸如介入性醫療器材、半導體晶片及噴射渦輪葉片等產品，皆為需要高度製程與檢測工具性能方可生產的範例，此趨勢代表機台製造商需對元件級誤差有深入的理解，才能打造出高精度的製造與測試系統，而要理解這些誤差，首先必須掌握工具或儀器的功能點誤差性能，表 1 列舉了幾個具體的應用範例，並說明相關的關鍵性能要求及這些誤差所帶來的影響。

表 1. 應用範例以及影響製程性能的運動誤差類型。

在設計機台時，回授裝置（例如雷射干涉儀或編碼器）對於量測移動軸的位置是必要的，然而，這些裝置本身存在著必須管理的內在誤差，此外，各移動軸的誤差運動 (Parasitic Motion) 未必能被回授裝置偵測到，卻仍會對整體的功能點誤差產生影響，隨著機台中移動軸數量的增加，可能的誤差源總數也隨之上升，系統中的每個元件軸在各運動方向上，皆可能存在六個主要誤差，包括三個線性誤差與三個旋轉誤差。

表 1 中的應用展示了一些簡單的範例，說明運動誤差如何影響特定製程的產出，對儀器設計者而言，對運動平台的系統性誤差進行詳細分析，能提供關於工具靈敏度的重要資訊，並最終引導其做出更佳、更精確的設計決策。

在實際的機台或儀器中，運動誤差通常僅為機台總誤差預算的一部分，其他與溫度、機台及工件安裝、地面振動、聲學振動等相關的誤差，也都會影響整體的誤差預算，此篇文章僅聚焦於多軸運動的誤差預算，然而，本文中所使用的方法同樣可以延伸應用於其他誤差源，以對機台或儀器執行完整的誤差預算分析。

運動誤差的定義以及如何在誤差預算中納入考量？

要執行任何誤差預算，必須先建立一個座標參考框架，並定義每個誤差相對於該框架的意義，圖 1 展示了所使用的座標系統，其中 A、B、C 分別用於表示環繞 X、Y、Z 軸的旋轉。

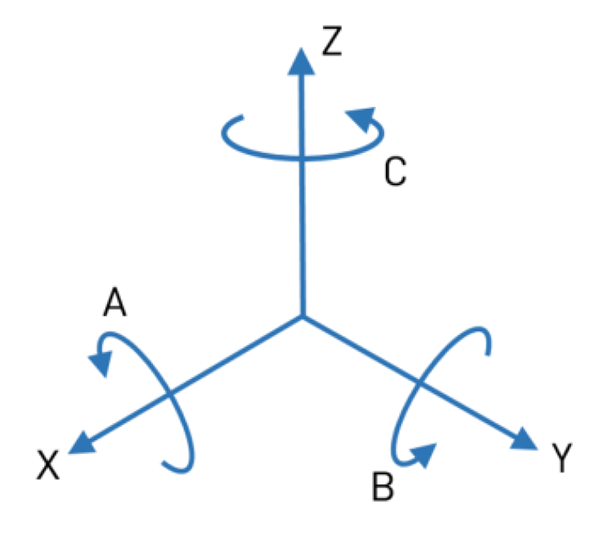
圖 1. 多軸誤差預算參考座標系統。

描述運動系統中誤差的通用慣例為：

EIJ = 由 J 軸所引起的 I 方向誤差 (1)
此處的 I 和 J 為廣義的方向與軸，在這個特定範例中，I 和 J 可以是 X、Y、Z、A、B 或 C。

表 2 展示了用以描述線性 X 軸與旋轉 C 軸所發生誤差的慣例。

表 2. 線性軸與旋轉軸的誤差慣例。

在建立座標系統與誤差慣例之後，必須先理解特定的機台特性，才能對多軸系統的誤差進行估算，這些特性如下：

1. 機台配置：
   a) 機台是如何配置的（例如，系統中與量測或製造過程直接相關的總軸數是多少）。
2. 軸向配置：
   a) 運動軸彼此的相對位置為何（亦即，這些軸是堆疊配置，還是分離配置，例如分離軸式）。
3. 製程點：
   a) 功能點（例如刀具點或工作點）、工作平面或工作體積相對於運動軸的位置在哪裡。
4. 製程敏感方向：
   a) 製程對哪個或哪些方向敏感（例如，雷射切割中的 X 與 Y 方向，或表面計量學中的 Z 方向等）。
5. 製程關鍵誤差：
   a) 每個軸在所有適用的自由度（DOF）下的元件誤差為何，以及軸間誤差（例如 X 軸與 Y 軸之間的垂直度）為何。

為闡明誤差預算過程，圖 2 展示了一個具有兩個運動軸的應用範例，此範例為一個直徑 300 mm 工件的檢測流程，感測器的定位方式，使其量測軸線位於代表受測工件直徑的線段上。

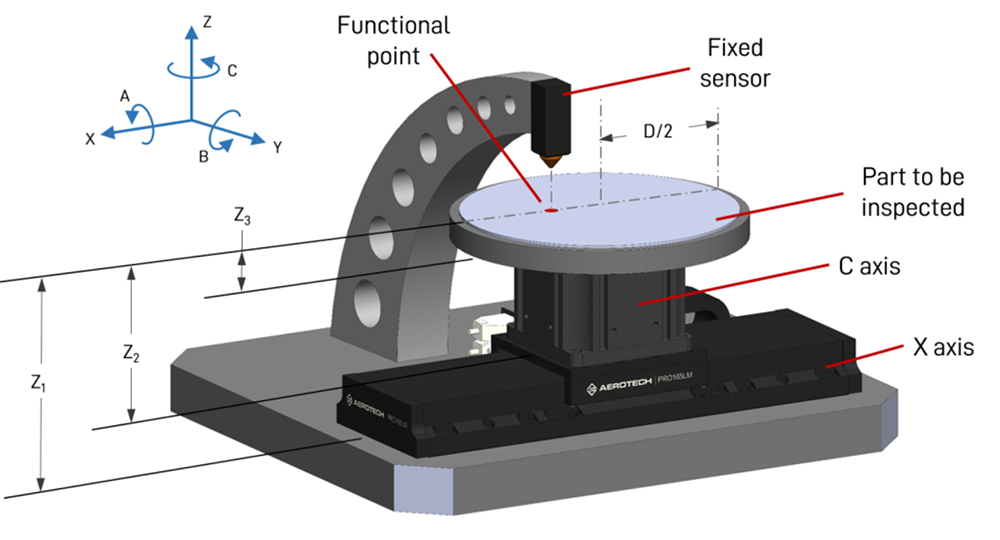
圖 2. 用於誤差預算分析的系統與應用範例。

回答上述五個問題，有助於確立在誤差預算過程中必須納入考量的關鍵誤差。

1. 機台配置：
   a) 雙軸零件檢測，採工件移動、製程頭固定的方式。
2. 軸向配置：
   a) 採 X-C 軸堆疊式結構，並整合夾頭用以固定直徑 300 mm 的工件。
3. 製程點：
   a) 功能點（例如製程點）位於直徑 300 mm（D）工件的頂部表面，此頂部表面距離平台安裝面為 Z1，距離 X 軸桌面為 Z2，並距離 C 軸軸心安裝面為 Z3。
4. 製程敏感方向：
   a) 感測器僅量測 Z 方向的位移，對於 X 與 Y 方向的誤差「不敏感」，雖然 X 和 Y 方向可能存在誤差，但此範例僅關注 Z 方向的誤差。
5. 製程關鍵誤差：
   
   a) 在此製程中，僅有發生在 Z 方向的誤差是關鍵的，這些誤差包括：
   
   i) EZX - X 軸的垂直直線度
   ii) EBX - X 軸的俯仰誤差
   iii) EZC - C 軸的軸向誤差運動
   iv) EBC - C 軸在 B 方向的傾斜誤差運動
   v) EC⟂X - C 軸旋轉軸相對於 X 軸行程的垂直度（對位）誤差
   
   b) 夾頭頂面與旋轉軸安裝面之間的平行度誤差，以及軸旋轉面的總偏擺（TIR, Total Indicator Reading），將會顯現為類似於傾斜誤差運動的「製程誤差」，但這些誤差是以每轉一圈的週期發生，為簡化說明，此處忽略這些誤差。

由於工件是在變動的半徑下進行量測，因此 X 軸的俯仰誤差（EBX）、C 軸的傾斜誤差運動（EBC）以及 C 軸與 X 軸之間的垂直度誤差（EC⟂X）都會影響量測結果，這些誤差的誇大示意圖如圖 3 所示。

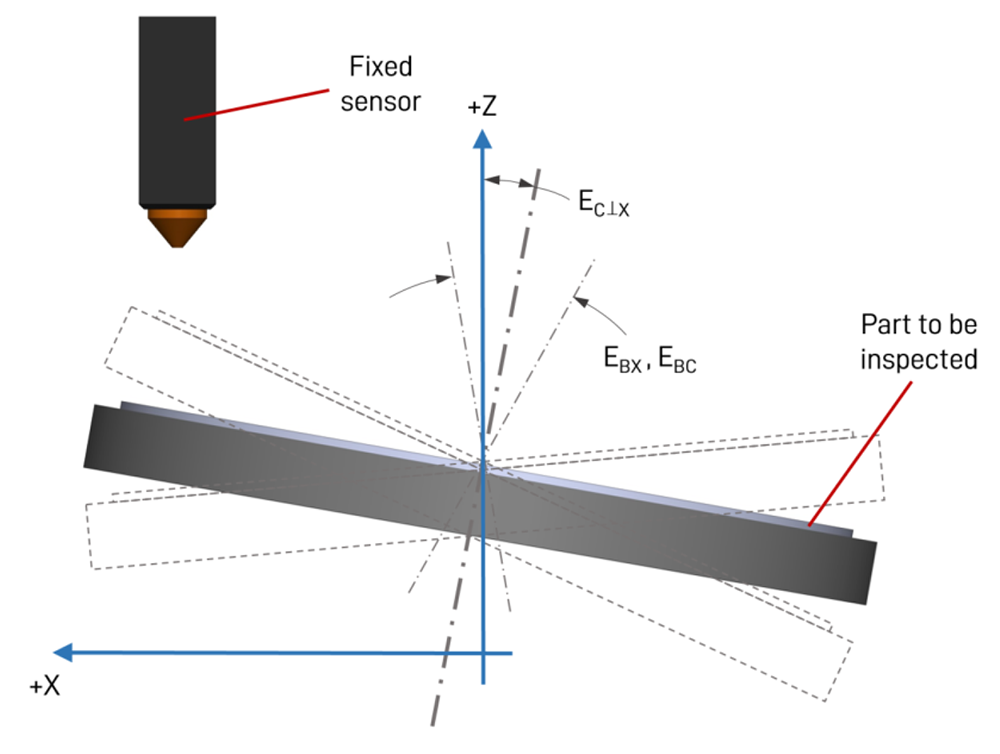
圖 3. X 軸俯仰誤差（EBX）、C 軸傾斜誤差運動（EBC）及 C 軸與 X 軸間垂直度誤差（EC⟂X）的誇大示意圖。

為了用數值執行實際的誤差預算，必須先知道個別的誤差值，透過多種計量技術（本文不深入探討），可以量測並量化這些誤差，本範例中使用的數值如表 3 所示。

表 3. 誤差預算分析中使用的範例尺寸與誤差值。

應如何整合各項誤差以評估系統級誤差？

在真實世界的運動系統中，表 3 中所示的峰值誤差很少會直接相加，雖然將峰值誤差直接加總或可提供系統級誤差的保守估計值，但這種方法往往會導致一個過度設計且成本高昂的運動系統，一個更為實用且常用的方法是以正交疊加方式加總誤差，正交疊加是一種用於組合兩個或多個不相關變數（在此案例中為誤差）的數學運算，採用正交疊加法，I 方向的誤差計算方式如下：

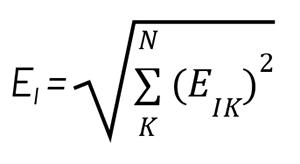(2)

其中 K 代表造成 I 方向誤差的來源，而 N 則是每個軸向對 I 方向誤差有貢獻的誤差數量。

X 軸的垂直直線度誤差 EZX 與 C 軸的軸向誤差運動 EZC 會直接影響 Z 方向的誤差（EZ），其他已識別的誤差（EBX、EBC 和 EC⟂X）則為角度誤差，它們只有在經過力臂放大後才會對 Z 方向誤差產生影響，如圖 3 所示，這些角度誤差可透過乘以適當的力臂距離轉換為 Z 方向的誤差，如下所示：

(3)

(4)

(5)

現在，Z 方向的總估計誤差可以寫成：

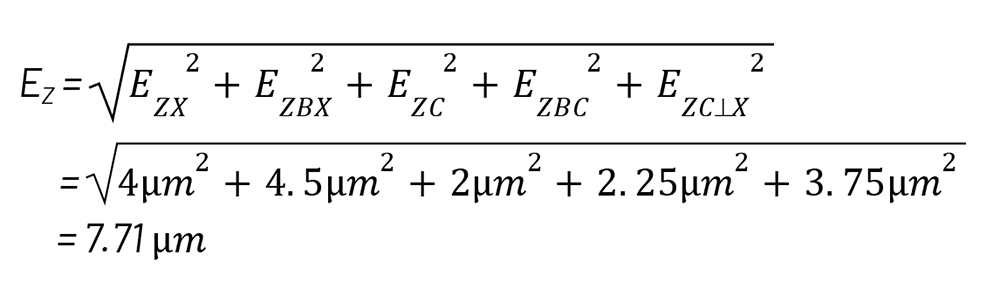(6)

在這個特定範例中，Z 方向的偏移量（Z1、Z2 和 Z3）並未納入誤差預算考量，然而，如果這是一個對 X 和 Y 方向誤差敏感的雷射切割製程，那麼這些偏移量就至關重要了。

雖然前述方法展示了估算特定製程中將出現誤差的方式，但它仍然代表總誤差的估計值，進一步延伸此概念，誤差值也可以是隨位置變化的函數或數值，相同的方法可用於更精確地表示運動系統工作體積內的誤差值，然而，由於計算量龐大，通常需要使用 Python™ 或 Matlab® 建構專用的機台模型，Slocum (1992) 提出了一種有效的方法，使用齊次變換矩陣（HTM, Homogeneous Transformation Matrices）來模擬機台誤差並執行多軸系統的誤差預算，這種方法可應用於從簡單到極其複雜的多軸系統。

本文所呈現的範例相對簡單，因為它僅涉及兩個軸與五個影響系統誤差的來源，現代機台通常使用更多的軸，且軸的排列可能變得非常複雜，此方法可以擴展至擁有多個軸的機台；然而，在「盤點」誤差時必須格外小心。

是否有方法能將誤差最小化？

在此範例中，Z 方向的總估計誤差為 7.71 μm，此誤差值依據期望的工件公差，可能顯得過大，在這種情況下，系統機台設計者必須重新檢視設計，以降低總誤差，誤差預算讓設計者能進行「假設」情境的模擬實驗，以判斷何處存在可改進的潛力，採用誤差較小的運動軸或將系統校準至更嚴格的公差可能成為必要手段，軸的排列與機台配置可能也需要重新評估，以找出更佳的幾何佈局，從而達成最終的目標誤差。

如果誤差具有可重複性，那麼透過獨立的量測裝置（如雷射干涉儀）進行量測並執行誤差補償或許是個合適的作法，在某些設計中，將量測裝置盡可能靠近功能點，或可實現誤差的即時量測與校正。

如何驗證預估的性能？

現代計量設備持續發展，為機台設計者提供多種量測系統性能的選項，然而，對於複雜的多軸系統，要執行真正的功能點量測可能非常困難且繁瑣，在檢測應用中，量測性能通常是透過量測已知標準件或已知良品來進行驗證，而對於加工或其他製造流程，通常是先加工零件，再使用外部量測工具進行量測以驗證性能。

然而，關鍵在於起始階段就採用能讓設計者估算系統級性能的方法與工具，在初期的誤差預算估算中捕捉更多細節，能提高機台設計者在最終設計中成功交付所需性能的機會。

結論

深入理解運動系統的應用、配置及相關的元件誤差，有助於對系統級誤差進行合理的估算，謹慎的元件誤差盤點，結合多軸誤差預算，為系統設計者提供了可用於改善系統性能的實用資訊，只要對元件誤差及其方向進行適當的記錄與管理，本文所示的方法便可應用於從簡單到複雜的各式系統。

參考文獻

Slocum, A. (1992). Precision Machine Design. Society of Manufacturing Engineers.

關於作者

John Lindell 是 Aerotech 的應用工程經理，擁有 22 年的精密運動控制經驗，他熱衷於理解、開發及部署用於測試與檢測應用的高精度運動系統，John 持有賓州州立大學的機械工程學士學位及匹茲堡大學的企業管理碩士學位。

相關產品

• 史都華六軸平台
• 平衡環轉台
• 運動控制龍門
• 客製化運動平台

延伸閱讀

以下文章深入探討了原文中提及的誤差分析、運動學、精度驗證與誤差最小化等技術，可作為進一步的參考：

• 伺服與振鏡組合運動精度評估：誤差特性分析與系統性能預測
• 五軸運動學實務：用 Transformation 函式處理座標轉換、偏移與動態加速度限制
• 非接觸式位移量測技術於精密運動控制系統之原理與應用
• 消除重複路徑的累積誤差：深入解析諧波消除與迭代學習控制技術
• 定位抖動的終極挑戰：三大平台實測，見證 Automation1 如何以 5 倍穩定性提升，碾壓前代效能！