技術文章

五軸運動學實務：用 Transformation 函式處理座標轉換、偏移與動態加速度限制

五軸運動學實務：用 Transformation 函式處理座標轉換、偏移與動態加速度限制

五軸運動控制是實現複雜曲面加工的關鍵技術，然而，將電腦輔助設計 (CAD) 中的理想路徑，精準轉換為真實機台的流暢運動，始終是一項艱鉅的挑戰，這其中不僅涉及複雜的運動學計算，更需要克服理論與現實世界之間的差距。

Aerotech Automation1 平台不僅是為了解決這個問題，更是為了重新定義五軸程式開發的效率與品質。我們的轉換函式深入考量了工程師在實務上會遇到的真正難題：

  • 輕鬆應對機械現實：
    文章不只介紹了理想化的旋轉，更透過直觀的 MatrixCreateTranslate() 指令，讓工程師能輕易設定與補償因機械組裝或工件夾持所產生的偏移量 (Offset)；現實世界中的誤差不再是繁瑣的程式補償，而是一個簡單的參數設定，大幅降低了設備校準的難度。
  • 克服加工品質的挑戰：
    我們深知在工件上維持恆定的加工速度，是確保曲面加工品質的大魔王，在平滑的工件路徑背後，往往是旋轉軸極劇烈的加減速，容易導致震動與精度下降；為此，Automation1 提供了如 TrajectoryFIRFilter 與 SetupDependentCoordinatedAccelLimit 等進階工具，賦予工程師「馴服」物理極限的能力，在追求高速的同時，確保無可比擬的加工品質。

這一切強大的功能，都被整合在設計清晰的 TransformationConfigure() 函式中，工程師不再需要手動計算和串接複雜的矩陣，而是能將精力完全專注於加工工藝本身，將開發時程從數月縮短到數天，有效降低技術門檻與開發成本。

本篇文章將帶您深入了解，如何運用這些強大的工具，從基本設定到進階優化，一步步釋放您五軸系統的全部潛力，實現更快的開發、更高的良率與前所未有的生產彈性。

Automation1 轉換函式

Automation1 中的轉換函式主要執行旋轉、鏡像和平移的矩陣運算，這些函式可用於轉換包含旋轉運動的機械致動器上的座標，對於擁有多個旋轉軸的系統，可以使用 TransformationConfigure() 函式設定多個旋轉矩陣，一個由兩個旋轉軸和三個線性軸組成的五軸系統便是這類系統的典型範例（如圖 1 所示），本篇應用說明將探討針對此類應用設定轉換函式的完整流程。


圖 1. 一個五軸組件的範例。

運作原理

五軸系統能夠讓刀具以垂直於曲面任一點的角度，存取該點在半球體上的任意位置，多數 3D CAD 工具都能夠輸出包含曲面上 x/y/z 座標位置的刀具路徑，並同時提供以兩個角度（如圖 2 中的 B 和 C 角度）表示的曲面法線向量。


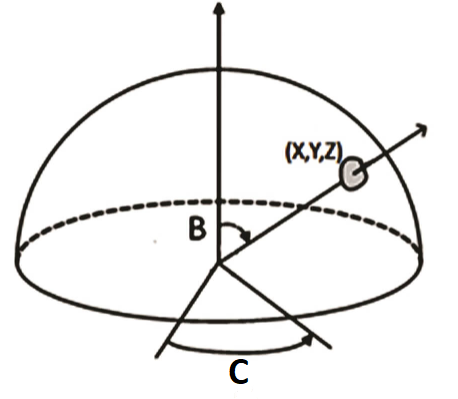
圖 2. 五軸系統能夠讓刀具以兩個角度位置表達的曲面法線，存取半球體上的任何點。

Aerotech 的轉換函式能夠即時擷取工件的 x/y/z 位置和旋轉角度資訊，並將其轉換為伺服軸的位置命令，由於工件位置與伺服系統位置有所不同，因此必須使用兩組軸，一組用來定義工件位置，另一組則用來定義伺服軸的位置，此處的工件軸系統由三個虛擬軸組成，在此範例中，我們將其命名為 x/y/z 軸，而實體軸則會對應至線性伺服軸 X/Y/Z 與旋轉軸 B/C。

右手定則

軸向的定義遵循右手定則，其中三軸中的第一軸指向食指方向，第二軸指向中指方向，而第三軸則指向拇指方向（如圖 3A 所示）。


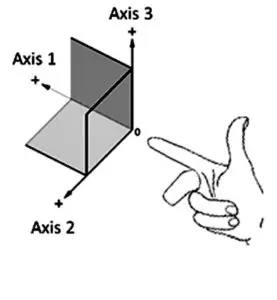
圖 3A. 右手定則座標系統。

此系統的旋轉發生在第三軸周圍，軸的正向旋轉方向同樣由右手定則定義，其中右手的拇指指向第三軸的正方向，而彎曲的手指則指示正角度的旋轉方向（如圖 3B 所示）。


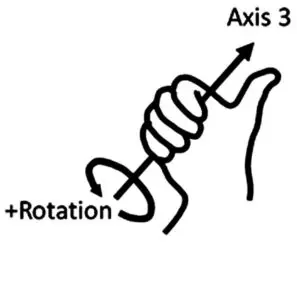
圖 3B. 右手定則的正向旋轉方向。

在定義虛擬軸與實體軸的正向移動方向時，必須嚴格遵守這些對應關係，輸入軸到輸出軸的映射過程，是從虛擬座標系統開始反向推導至實體軸，在此過程的每一步，所映射軸的正向移動方向，都必須彼此保持一致，並且符合右手定則。

圖 4 中展示的方向是四種可能配置之一，其餘三種配置可透過將 x/y 平面繞 z 軸以 90 度為間隔旋轉而獲得，任一系統中的軸名稱皆可依據應用需求進行更改。
極度重要： 軸的正向運動定義已由圖示中的箭頭方向固定，一旦座標框架設定完成，軸或工件程式的正向移動方向就必須修改，以確保其與座標框架所指示的方向一致。


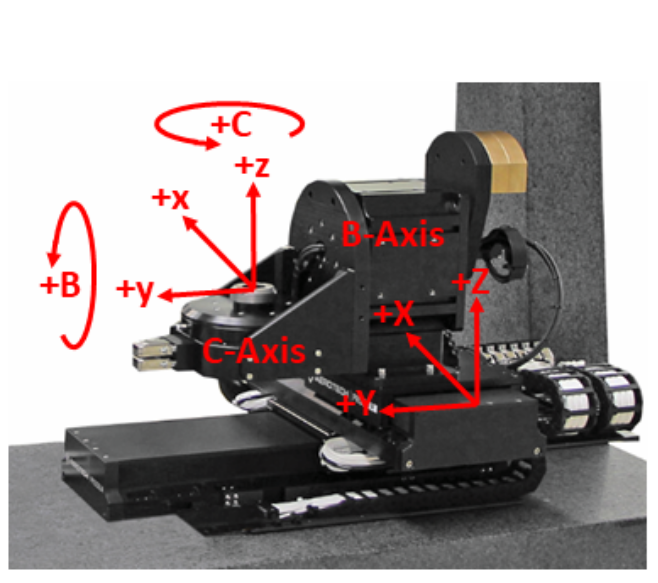
圖 4. 一個顯示軸向的五軸系統範例。

依照我們在圖 4 中定義的映射關係，在沒有任何旋轉作用的情況下，+x 方向的運動將導致 +X 方向的運動，+y 方向的運動將導致 +Y 方向的運動，而 +z 方向的運動將導致 +Z 方向的運動。

設定 TransformationConfigure() 函式

系統最多可同時執行 32 個矩陣轉換，在此案例中，TransformationConfigure() 函式將負責設定轉換，並將資料從一個三軸笛卡爾座標系統（InputAxes）轉換到另一個三軸系統（OutputAxes），每個 TransformationConfigure() 函式中最多可同時存在 512 個矩陣，此範例僅需為多個矩陣設定一個 TransformationConfigure() 函式。

對於圖 4 所示的系統，第一個旋轉軸是 B 軸，它在 z/x 平面內繞著我們輸入平面的 y 軸旋轉，根據右手定則，正向旋轉運動為逆時針方向，下一個旋轉軸是 C 軸，它使 x/y 平面繞 z 軸旋轉，其正向旋轉運動同樣為逆時針方向，旋轉矩陣的指定方式如下：

  • MatrixCreateRotateJ(B) – 建立一個繞第二輸入軸（y 軸）旋轉的矩陣；旋轉角度由旋轉軸 B 決定。
  • MatrixCreateRotateK(C) – 建立一個繞第三輸入軸（z 軸）旋轉的矩陣；旋轉角度由旋轉軸 C 決定。

因此，用於旋轉矩陣的 TransformationConfigure() 函式如下所示：
TransformationConfigure(0, [MatrixCreateRotateJ(B), MatrixCreateRotateK(C)], [x, y, z], [X, Y, Z])

此處的 [x, y, z] 是輸入軸，由工件位置的三個虛擬軸定義，而 [X, Y, Z] 是輸出軸，由線性伺服系統的三個實體軸位置定義。

設定偏移量

在多數應用中，旋轉軸的旋轉中心彼此之間存在偏移，此外，工件座標系統的原點可能不會直接位於旋轉軸的中心上，如圖 5 所示，MatrixCreateTranslate() 矩陣即是用於定義旋轉軸與工件座標系統之間的偏移量，此位移命令包含所有三軸的偏移值，偏移量的計算是根據從參考點到旋轉點的距離，而位移的正負號則是根據從參考點移動至旋轉點的方向來決定。


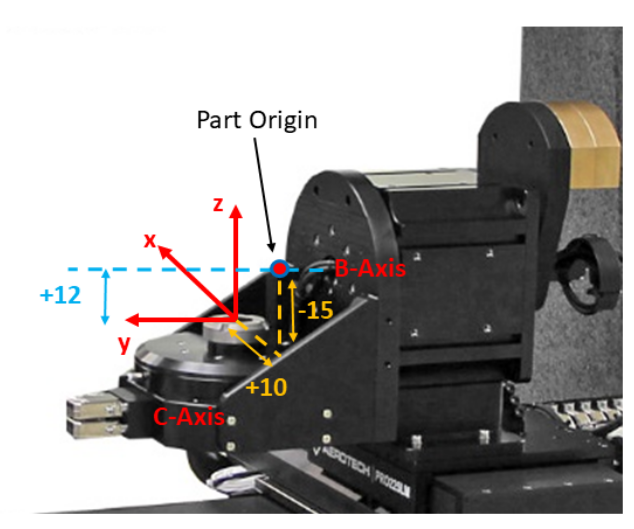
圖 5. 設定偏移量。

以我們的範例系統為例，假設 B 軸和 C 軸的旋轉中心相交，工件原點在 C 軸檯面上方偏移 15 mm，並在 x 方向偏移 10 mm，而 B 軸的旋轉中心與 y 軸平行且共線，並位於 y 軸上方 12 mm 處，在此配置下，旋轉命令的偏移量如圖 5 所示。

要計算 B 軸繞 y 軸旋轉的偏移量，B 軸的座標框架必須放置在其旋轉軸上，此座標框架的原點可位於旋轉軸上的任何位置，因為沿 B 軸的角度位置不會因旋轉原點的位置而改變，舉例來說，如果一根圓管繞其中心旋轉，管上任何一點的角度位置都不會因為施加旋轉的點在管上的位置不同而改變（如圖 6 所示）。


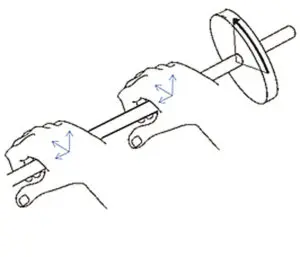
圖 6. 顯示 B 軸偏移與其旋轉軸上位置無關的範例。

因此，我們可以將 B 軸的旋轉點原點直接放置在 C 軸旋轉點的正上方，這使得 x 和 y 方向的偏移量為「0」，z 方向的偏移量則為 +12，因為我們從 C 軸表面的起始點沿 +z 方向移動至 B 軸的旋轉中心，這些偏移量需按照 MatrixCreateTranslate() 矩陣中定義的軸順序來放置，用於 B 軸第一次旋轉的 MatrixCreateTranslate() 如下：

MatrixCreateTranslate(0, 0, 12)

C 軸旋轉的偏移量也用類似的方式計算，從圖中可知，從工件原點到 C 軸旋轉中心沿 x 軸方向的距離為 +10，沿 z 軸方向從工件原點到旋轉中心的距離為 -15，工件原點與 y 軸共線，因此該方向的偏移量為 0。

設定 C 軸旋轉偏移的方式如下：
MatrixCreateTranslate(10, 0, -15)

將偏移矩陣應用於同一個 TransformationConfigure() 函式後，最終的 TransformationConfigure() 函式如下所示：
TransformationConfigure(0, [MatrixCreateRotateJ(B), MatrixCreateTranslate(0, 0, 12), MatrixCreateRotateK(C), MatrixCreateTranslate(10, 0, -15)], [x, y, z], [X, Y, Z])

請注意，MatrixCreateTranslate() 矩陣的放置順序是特定的，以確保偏移量能對應到其相應的旋轉矩陣，在此範例中，MatrixCreateTranslate(0, 0, 12) 緊跟在 MatrixCreateRotateJ(B) 之後，因為它是為 B 軸旋轉計算的偏移量。

轉換函式設定完成後，可使用以下命令來啟用或禁用轉換功能：
TransformationEnable()
TransformationDisable()

恆定速度與曲面速率的相關議題

當在 Automation1 中透過 VelocityBlendingOn() 函式啟用輪廓加工時，控制器將依據任務的加速度參數來提升向量速度，直到達到由「F」碼設定的程式向量速度為止，此速度將在整個程式執行過程中保持，除非遇到強制減速的條件，然而在工件上保持恆定速度，對伺服軸的運動有著重大影響，因為它們可能需要瞬間改變速度或方向。

標準的前瞻（Look-Ahead）功能，雖然能夠監測圓弧中的加速度或偵測兩程式行之間的非相切移動，但無法直接解決這個問題，因為這些加速度是由轉換函式間接產生的，現有兩種額外的方法可用於限制實體軸的加速度。

第一種方法是在伺服軸的速度命令流上使用一個濾波器，此濾波器產生的效果類似於斜坡功能，但它也會在輪廓中增加延遲，從而導致路徑偏離程式設定的路徑，TrajectoryFIRFilter 用於設定應用於速度命令流的 FIR (Finite Impulse Response，有限脈衝響應) 濾波器長度，濾波器中的每一個「Tap」相當於 0.125 毫秒的時間間隔，若要增加 50 毫秒的濾波時間，參數應設定為 50 / 0.125 = 400。

第二種降低加速度的方法是設定相依軸的加速度限制，B 軸和 C 軸被視為相依軸，因為它們的速度命令是從虛擬的 x/y/z 軸推導而來，x/y/z 軸的短移動時間，若耦合 B/C 軸的長距離移動，可能導致 B/C 軸產生極高的速度，SetupDependentCoordinatedAccelLimit() 函式可用於限制相依軸的加速度及因此產生的速度。

程式範例

以下為一個簡易範例，展示了所有命令的執行順序，並包含了相依軸加速度限制的設定。


program

TransformationDisable(0) // 重置並禁用轉換函式
Enable ([X, Y, Z, x, y, z, B, C])
Home ([X, Y, Z, x, y, z, B, C])
VelocityBlendingOn() // 啟用速度輪廓模式
SetupDependentCoordinatedRampRate(500) // 設定協同加減速率
SetupDependentCoordinatedAccelLimit(4000) // 設定相依軸的加速度限制
SetupTaskTimeUnits(TimeUnits.Seconds) // 將進給率單位設定為每秒距離單位
F100 // 指定協同運動中相依軸的進給率
G90 // 設定絕對定位目標模式

/* 開始設定轉換矩陣
[x, y, z] 是輸入軸；[X, Y, Z] 是輸出軸。
MatrixCreateRotateJ 繞第二輸入軸 y 軸旋轉一個角度；角度由旋轉軸 B 決定
MatrixCreateRotateK 繞第三輸入軸 z 軸旋轉一個角度；角度由旋轉軸 C 決定
MatrixCreateTranslate 定義輸入軸的偏移值
*/
TransformationConfigure(0, [MatrixCreateRotateJ(B), MatrixCreateTranslate(0, 0, 12), MatrixCreateRotateK(C), MatrixCreateTranslate(10, 0, -15)], [x, y, z], [X, Y, Z])

// 移動實體軸 X/Y/Z 至起始位置
G0 X5 Y60 Z23
// 移動旋轉軸至起始位置
G0 B0 C0
// 移動虛擬軸至起始位置
G0 x9 y0

AppDataCollectionSnapshot()

// 開始旋轉轉換
TransformationEnable(0)
G1 x10 y2 z1 B3 C2
G1 x12 y3 z1.4 B3.7 C2.5
G1 x9 y2 z1.8 B3.8 C1.5
G1 x8 y2 z2.2 B0 C0
TransformationDisable(0)
AppDataCollectionStop()
VelocityBlendingOff()

end

相關產品

延伸閱讀

 

回上頁