技術文章

雷射干涉儀回饋下的機台定位不確定性分析

透過雷射干涉儀回饋，解析機台定位的不確定性

雷射干涉儀回饋在許多高精度系統中扮演著不可或缺的角色，它確保機台在微米甚至奈米級的精確度下運行，然而，即使是最精密的系統也難免受到各種因素影響，導致定位產生不確定性；對於追求極致精度的產業來說，這無疑是一大挑戰，這些不確定性可能導致產品良率下降、製程效率降低，甚至影響最終產品的效能與可靠性；本文將闡述具備接近量測點（work point）雷射干涉儀回饋系統中，造成機台定位不確定性的主要因素，並透過實例，量化雷射回饋驅動機台中這些不確定性的具體數值。

在許多製造高精度運動系統的過程中，雷射干涉儀常用來校正機台和驗證精度，在受控制的環境條件下，雷射干涉儀的量測不確定性，會比一般常用運動控制設備所能達到的精度還要低，所以，當製造過程需要極高精確度時，雷射干涉儀常被用在接近機台量測點的地方，作為機台控制的回饋機制；在這些情況下，當機台的運動本身就已經非常精確時，如果用來量測它的雷射干涉儀不夠「準」，它的「不確定性」跟機台本身的「運動誤差」差不多甚至更大時，那這個雷射干涉儀的量測結果，就不能真正地告訴你機台到底有多精準，反而會因為量測工具本身的限制而失去判斷價值。

本文將解釋在使用接近量測點的雷射干涉儀回饋系統中，哪些是造成機台定位不確定性的主要因素，透過一個實際案例，量化雷射回饋驅動機台中這些不確定性的具體數值，這並非量測不確定性、雷射干涉儀回饋、誤差/不確定性預算或是剛體運動誤差的入門介紹，而是概述在特定機台設計中，量測點位置可以達到的量測不確定性程度。

雷射回饋系統中主要的不確定性來源

採用雷射干涉儀回饋裝置的運動系統，存在多個不確定性來源，雖然差動熱膨脹、阿貝誤差（Abbe offsets）、光學元件品質、回饋迴路中的雜訊，以及系統的物理設定等因素，也會造成實質性的影響，但大部分主要的不確定性來源，都與環境有關；因此，要在這類系統中實現超精密運動，了解並盡量減少這些因素對特定量測的影響，至關重要。

在使用干涉儀回饋時，最需要關注的是雷射周圍的環境，光的波長是與基本運動單位「公尺」連結的基礎，它會隨著光線穿過介質的折射率變化而改變，在空氣中，折射率會隨著溫度、壓力、濕度，甚至空氣局部成分的變化而明顯改變，結果是，要進行精確的定位量測，就需要持續且準確地掌握這些環境參數，以便進行主動波長補償；此外，雷射光束上氣流的速度和類型，會導致折射率的局部波動，進而產生量測雜訊。

除了與環境相關的因素，影響機台運動整體不確定性的還有幾個其他因素，干涉量測系統中使用的平面反射鏡的光學平坦度與對準度，會造成量測點運動的不確定性；同樣地，在干涉儀與定義量測點之間，任何微小的阿貝誤差，角度誤差運動的影響都可能是一個主要因素；在不確定度預算較低的情況下，雷射波長穩定性和校準精度是一個不能忽略的因素；當使用外差式雷射（heterodyne laser）時，頻率洩漏（frequency bleed through）也會導致顯著的量測不確定性；最後，就像幾乎所有精密機台一樣，任何元件在未經補償的距離上的熱膨脹，都會給量測點的運動控制帶來顯著的不確定性；圖1顯示了在接近量測點使用等外差雷射干涉儀（homodyne laser interferometer）回饋的機台中，造成運動控制主要不確定性因素的圖表。


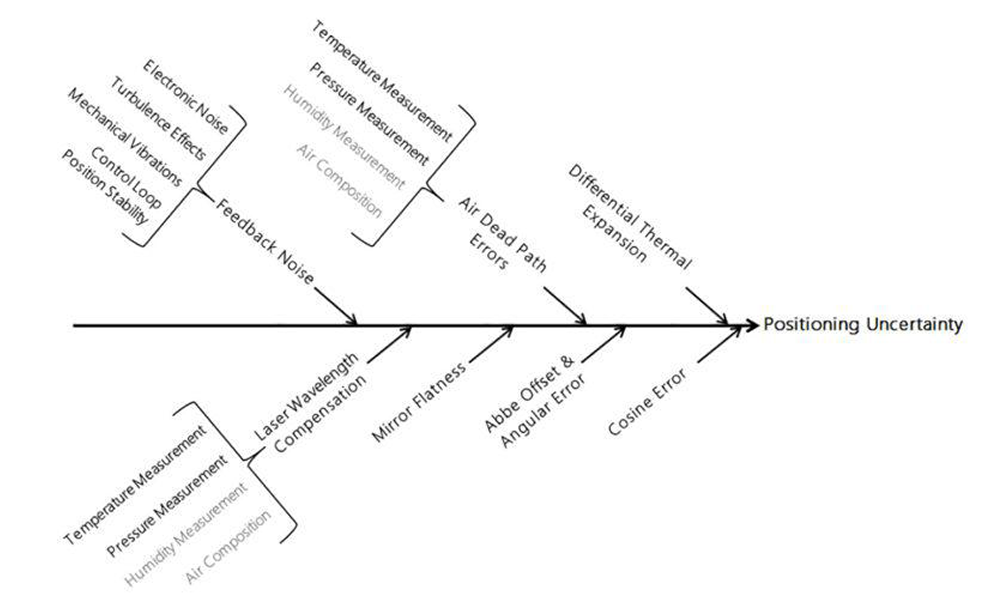
圖1：精密運動控制設備中，等外差雷射干涉儀回饋量測量測點運動的主要不確定性因素圖，部分因素未明確列出，包括雷射頭溫度敏感度，以及許多用於計算的額定常數相關的不確定性。

量化範例機台的定位不確定性

圖1中列出的不確定性因素影響程度，會因為每台機台的設計、行程長度、環境以及其定義的量測點而有所不同，量化這些影響只能在知道機台具體細節的情況下，才能逐一估計，即使機台與之前分析過的相似，每種機台設計都必須有自己的不確定性分析；因此，我們將以 Aerotech 總部用於量測工具的機器視覺檢測站的運動作為具體範例，來估計量測不確定性。圖2顯示了目前安裝在 Aerotech 量測實驗室中的機台。


圖2：一台安裝在溫控環境中的精密檢測機範例，平面反射鏡整合在負載板中，為運動控制提供量測點平面的雷射干涉儀回饋。

圖2所示的檢測站設計有一個大型負載板，這個負載板不僅承載用於固定基板的真空吸盤，還包含兩個用於在量測點提供雷射干涉儀回饋的平面反射鏡，在評估雷射量測量測點運動的不確定性時，該機種包含了圖1中所有列出的主要影響因素，透過逐一分析這些來源，我們可以為此特定機台應用，獲得合理的量測不確定性估計；如同所有工程任務，在量化不確定性時必須做出某些假設，而這些假設的有效性，則取決於特定應用所需達到的不確定性或誤差預算；這種針對特定應用的深入分析，是每個機台設計，更具體地說，每個機台任務都應該有自己不確定性分析的另一個重要原因。

量測目標的定義

我們要強調一個非常重要的觀念，但它也常被大家搞混：「不確定性分析」永遠是針對特定的「量測」行為；意思是機台或設備本身並不會有「不確定性」；只有當你用它來量測某個具體、明確定義的「東西」時，這個「量測」的結果才會帶有不確定性，因此，清楚定義要量測的是什麼（也就是「量測目標」），對於後續量化這個量測的不確定性來說，影響非常大；在此討論的範例中，量測目標定義為透過兩個獨立的平面反射鏡干涉儀對量測點位置進行的二維平面量測。為了使此量測目標有意義，機台的量測點必須被明確定義。

圖2中所示的機器視覺檢測站的量測點（或原點），定義為相機光軸與平行於真空吸盤安裝表面最小二乘平面擬合的平面之交點，且該平面僅比真空吸盤高出 3 毫米；這個「浮動」平面的垂直位置，取決於該機種設計用來量測的零件的典型厚度，因此，真空吸盤表面加上 3 毫米的偏移量，定義了 XY 座標平面，使其與標準待測物的上表面名義上重合；X軸運動定義為：X反射鏡表面最佳擬合平面的單位法向量，投影到由偏移真空吸盤表面定義的XY座標平面上；最後，Y軸運動定義為：真空吸盤安裝平面單位法向量與X軸單位向量的向量積，所有這些都以相機光軸的交點作為原點；圖3顯示了該機種量測點的示意圖。


圖3：光學三次元量測儀（CMM）量測點示意圖：XY 平面由真空吸盤的安裝表面決定，原點由相機光軸與此 XY 平面的交點決定，X 軸方向由 X 反射鏡表面的單位法向量決定；最後 Z 軸是 XY 平面的單位法向量，Y 軸方向是 Z 和 X 單位向量的叉積，這定義了量測點和量測座標系。

解析度與回饋雜訊

需要量化的前兩個主要不確定性因素是量測系統的解析度和回饋雜訊底線，干涉儀的解析度很容易確定，因為它是由製造商的電子硬體決定的，並且應該在相關的操作手冊中說明；該機種採用 Renishaw RLD 雙程平面反射鏡干涉儀，具有 10 奈米的數位量測解析度，假設為方型分佈寬度。

回饋雜訊底線將決定機台的最小有效解析度，並為量測量測點平面運動的不確定性設定了下限；如圖1所示，在這種情況下，回饋雜訊主要受電子雜訊、機械振動、控制迴路穩定性，以及影響最大的跨開放式干涉儀光束的空氣湍流所主導；在此機種中，透過使用高順應性被動空氣隔離系統，最大程度地減少了機械振動對干涉儀的影響；同樣，三次元量測儀（CMM）本身被封閉在環境控制外殼裡，以最大程度地減少穿過雷射光束的氣流，該機種的整體實施，產生了約 25 奈米均方根的長期（超過3小時）雷射穩定性。

雷射波長補償與無效路徑誤差

正如前面提到的，與基本量測單位「公尺」的連結，就是系統中使用的光的波長。波長會因為光線傳播介質中折射率的偏差而改變，所以這些變化都必須被補償。

雷射波長會隨著局部環境變化而改變，需要對此進行補償，而這個需求很早以前就已經有相關文獻（文獻1）詳細記載了，並且是大多數市售干涉儀系統的自動化功能，在這種情況下，濕度和空氣成分的變化小到可以忽略；然而，波長補償（以及因此的干涉量測本身）的準確性/不確定性，取決於能否精確量測剩餘環境參數（溫度和壓力）的變化。

當應用於距離量測時，比如在此機種中，干涉量測是相對於某個參考位置執行的，因此，波長補償僅主動應用於檢測器在離開參考位置時所計數的條紋或波數。實際上，雷射頭在參考位置時無法與反射鏡直接接觸，必須提供一些緩衝空間。總會有一小部分雷射光束的波長補償沒有被計算在內。當局部環境改變時，這段光束的長度沒有得到補償，就會導致系統零點位置的小幅偏移，這稱為無效路徑誤差（dead path error）。

由於省略波長補償所造成的誤差與長度相關，因此，將每個雷射頭與參考點處反射鏡位置之間的空間量降到最低，就能最大程度地減少無效路徑誤差導致的不確定性。

雷射波長補償和無效路徑對量測點量測不確定性的影響都與長度相關，因此，在此量化範例中，我們會考慮它們在最大操作距離上的影響，該機種用於校正環境相關波長變化的氣象站，其絕對溫度精度為 0.2°C，絕對壓力精度為 1 mbar，在3小時的測試中，溫度和壓力的相對變化（會影響無效路徑誤差），分別被觀察到小於 0.1°C 和 0.5 mbar；為了簡化起見，這些值對量測不確定性的影響，可以透過根據 ASME 標準2, 3的最新雷射比例校正靈敏度係數進行量化，這樣就可以避免根據量測不確定度表示指南（GUM）4和經過校正的 Edlen 方程式5來執行不確定度傳播分析。

假設機台在標準溫度、壓力、濕度下運行，氣象站溫度和壓力量測精度對不確定性的貢獻，在機台 300 mm 的完整行程範圍內，分別為 29 奈米和 5 奈米。同樣，在給定測試中，溫度和壓力的相對變化分別對每軸 96 mm 的無效路徑產生 5 奈米和 1 奈米的量測不確定性，這些貢獻都被視為方型分佈寬度，有關雷射波長補償和無效路徑誤差的更詳盡解釋，可在 Renishaw 技術文件 TE3296中找到。

反射鏡平坦度、正交性與餘弦誤差

相較於雷射波長變化的影響，反射鏡平坦度和機械對準對量測不確定性的影響更為直接，每個反射鏡的平坦度會直接造成量測點的定位不確定性，這體現在直線度誤差（straightness errors）上；此外，如果反射鏡的表面法線與定義的 XY 座標平面沒有對齊，將在 X 軸和 Y 軸的量測刻度中引入餘弦誤差；同樣地，即使反射鏡對齊了，雷射光束本身若未對準每個反射鏡的法線，也會引起餘弦誤差；最後，兩個反射鏡表面之間若沒有精準的正交性（垂直），將對量測點的位置量測產生垂直度誤差（squareness error）。

從量化數據來看，該機種使用的反射鏡，其整個表面的峰谷平坦度規範為 63 奈米，這項規格在驗證報告中達到了 95% 的信賴區間（confidence interval），透過精密的機械夾具和加工製程，我們確保反射鏡的法線與 XY 座標平面的對準誤差小於 25 µrad；同時，根據實際行程中觀察到的訊號變化，雷射光束與反射鏡的對準誤差也小於 25 µrad；最後，兩個反射鏡彼此的正交性則透過正方形參考物件和反向技術進行軟體校正；經過校正，反向操作所帶來的不確定性，使得反射鏡之間的垂直度誤差小於 0.05 µrad；綜合這些因素，反射鏡平坦度規格會導致 16 奈米的量測不確定性；反射鏡和雷射對準所造成的餘弦誤差，在機台整個行程中，各貢獻 0.1 奈米的量測不確定性；而兩個反射鏡的正交性，則會在機台的操作範圍內，產生 15 奈米的三角形不確定性分佈。

阿貝誤差與角度誤差

角度誤差運動對量測點位置量測不確定性的影響，通常是最大的因素之一，這是因為量測點與定義的目標量測點之間，經常包含阿貝誤差（Abbe offset），在接近或於量測點使用干涉儀回饋的主要原因之一，是為了消除阿貝誤差，進而消除角度誤差運動對量測點量測的影響；在此特定範例中，雷射光束定位、回饋機制與定義的量測點之間，名義上沒有阿貝誤差；因此，由軸承導軌的角度誤差運動所造成的量測不確定性可以忽略不計；然而，為展示最小化阿貝誤差的重要性，僅 10 毫米的阿貝誤差，對於 25 µrad的角度誤差運動，即可導致 250 奈米的量測不確定性。

機械零件的差動熱膨脹

最後，各種機械零件的差動熱膨脹對量測不確定性有著顯著的影響，例如，由於該機種的量測點定義，每個雷射頭與量測點之間有一大段花崗岩，這段花崗岩會隨著溫度變化而自由膨脹和收縮，如果在測試過程中，花崗岩機台基座的溫度發生變化，支撐相機的花崗岩橋將會膨脹或收縮，使光軸相對於雷射頭發生位移；然而，干涉儀系統的回饋控制將維持每個反射鏡與每個雷射頭之間的相同距離，這將導致量測點發生偏移，而讀數卻沒有顯示出位置變化，因此在量測過程中會增加量測不確定性。

然而，在此特定機台設計中，反射鏡面與量測點之間，以負載板形式存在的鋁材長度較短，它也會隨溫度變化而膨脹和收縮，經設計，當花崗岩和鋁材同時膨脹和收縮時，它們的長度對量測點運動相對於網格板上量測到的位置，貢獻了相反的方向，因此，只要鋁材與花崗岩的長度比率，與它們各自的熱膨脹係數比率相等，則每個機械零件的膨脹對待測零件的量測，其所貢獻的量測不確定性即可忽略不計。

總結與擴展標準不確定度

當組合不相關輸入的不確定性貢獻時，可以將其分佈的估計不確定性進行平方和開根號，這是 GUM4 中描述的不確定性傳播的簡化應用，並適用於本範例；表1總結了本分析中考慮的主要貢獻因素、其不確定性貢獻，以及系統定位量測中包含的組合和擴展不確定性；類似表1的不確定性摘要，可以深入了解應將精力集中在哪裡，以進一步改善量測。


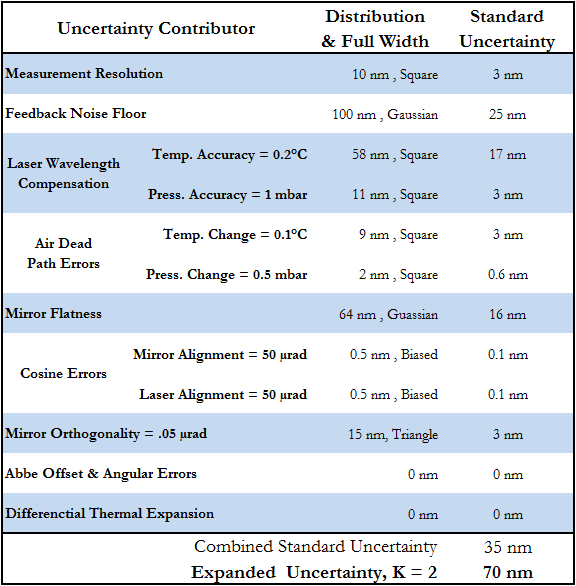
表1：量測不確定性因素摘要，以及量測點位置量測的擴展標準不確定性估計值。

值得注意的是，在此不確定性分析中，已經做了許多假設，同樣，分析的指導依據是大量的基本原理和背景知識；如前所述，每個機台設計都應附有其自身的不確定性預算和分析，圖1中概述的主要貢獻因素，對於其他情況可能不夠詳盡，且在所需量測不確定性較低的水準下，所做的簡化假設可能不適用，為了更好地理解量測不確定性及其估計，國際度量衡局網站（7）上免費提供的《量測不確定度表示指南》（GUM）及其補充材料4是一個很好的參考資料。

關於作者


William S. Land II 是 Aerotech 機械工程師暨行銷營運經理，負責管理其全球行銷營運的技術事務，在 Aerotech 工作了十多年，此前曾擔任各種工程、產品管理和業務開發職務，他擁有賓夕法尼亞州立大學機械工程學士學位和北卡羅來納大學夏洛特分校機械工程碩士學位。

相關產品

延伸閱讀

參考文獻

  1. Edlen, B. The refractivity of air. Metrologia, 1966.
  2. ASME B5.57. Methods for performance evaluation of computer numerically controlled lathes and turning centers. American Society of Mechanical Engineers, New York, 1998.
  3. ASME B89.1.8. Performance evaluation of displacement measuring laser interferometers. American Society of Mechanical Engineers, New York, 1998.
  4. Bureau International des Poids et Mesures, Commission électrotechnique internationale, and Organisation internationale de normalisation. Guide to the Expression of Uncertainty in Measurement. International Organization for Standardization, 1995.
  5. Birch, K. P., and M. J. Downs. “Correction to the updated Edlén equation for the refractive index of air.” Metrologia 31.4 (1994): 315.
  6. Chapman, M.V. TE329: Environmental compensation of linear laser interferometer readings. Renishaw Technical White Papers.
  7. Bureau International des Poids et Mesures. http://www.bipm.org/en/publications/guides/
回上頁