精密運動控制再進化
諧波消除技術克服航空航太與國防應用的週期性擾動挑戰

消除週期誤差根源，達成奈米級運動精度

控制理論的內部模型原理 (Internal Model Principle) 指出，為求完美抑制輸入訊號而設計的演算法，必須包含該輸入訊號的模型；遵循此內部模型原理的回授控制，促進了諧波消除演算法，甚至更複雜的重複控制器 (Repetitive Controllers) 的發展。
 

它們有何用處？

精密運動控制中普遍存在的週期性擾動，可透過諧波消除演算法有效抑制，在精密運動控制應用中，週期性擾動十分常見；任何振盪或旋轉運動都會在主動和輔助運動軸中產生某些週期性誤差，諧波消除演算法若應用得當，能為控制系統工程師提供一種額外的工具，此工具不僅有效，且易於使用常見的頻域分析技術進行分析，用以消除精密運動系統中的追蹤誤差，它們適用於伺服命令或擾動主要為週期性時，例如在工具機、資料儲存系統以及感測器測試 (sensor testing) 等應用；由於遵循內部模型原理的控制器包含了系統輸入的模型，因此諧波消除演算法也包含了週期性訊號產生器，當與經過良好調整的傳統控制器結合時，這些演算法便成為伺服系統設計者相當有用的工具。
 

內部模型原理 (Internal Model Principle)

控制理論的核心概念之一，內部模型原理，要求控制器需內建輸入訊號模型以達成零誤差追蹤，此原理是一個看似簡單卻極為強大的概念，在 1970 年代中期首次被公式化，它要求演算法必須包含任何欲以零穩態誤差 (identically zero steady-state error) 追蹤的輸入訊號之產生器（或模型），圖 1 以方塊圖說明此概念；為了使命令參考訊號與量測訊號之間的誤差為零，控制演算法必須能夠在沒有任何進一步輸入的情況下自行產生此訊號；內部模型原理最常見的應用，是在普遍的 PID（比例-積分-微分）控制器中使用積分器 (Integrator, I) 項，考量一個以線性馬達驅動的定位平台，其模型為一個自由質量，並對其施加控制力：僅使用比例 (Proportional, P) 與微分 (Derivative, D) 控制已足以穩定系統；然而，任何恆定的擾動力量（來自製程、重力、纜線等）都會在參考位置與量測位置之間產生一些誤差，以供類似彈簧的比例控制項產生輸出；恆定擾動被模型化為一個步階輸入 (step input)，其拉普拉斯轉換 (Laplace transform) 為 1/s，將此項（即積分器）加入控制演算法中，允許輸出增長至一個恆定值，以抵銷擾動並達成零穩態誤差。
 

圖 1. 內部模型原理要求控制器包含輸入訊號的模型，以便在沒有任何穩態驅動誤差的情況下，產生適當的輸出。
 

重複控制器 (Repetitive Controllers)

為了處理週期性訊號，重複控制器利用內部訊號產生器滿足內部模型原理，在回授控制演算法中加入週期性訊號產生器，滿足了內部模型原理的要求，並能夠完美追蹤週期性命令以及完美抑制週期性擾動；這些演算法被稱為重複控制，最早於 1980 年代初期被定義，而內部模型原理正是這種「用於重複操作的控制器」的基礎；最初，開發人員使用在回授迴路中帶有延遲元件的控制器來形成週期性訊號產生器；然而，在連續時間域中，時間延遲元件對應到具有無限多個邊際穩定極點 (marginally stable poles) 的控制器（參見圖 2）；時域中具有任意急劇轉變的訊號，需要一個能夠產生這種高頻內容的高頻寬訊號產生器；穩定這些系統具有挑戰性，因為高頻控制器極點傾向於與伺服機構機械結構中未建模或可變的動態特性相互作用，從而導致不穩定；針對離散時間域中的重複控制演算法進行類似分析，也呈現出相同的問題；經典的傅立葉級數分析 (Fourier-series analyses) 闡明了時域中的重複序列與頻域中極點位置之間的關係；任何週期性訊號都可以同樣良好地表示為簡單振盪函數（即正弦波 (sinusoids)）的總和；簡言之，重複控制器（應用於線性系統時）可被視為一系列單頻振盪器被加入控制演算法中，用以消除本身即為單頻正弦波總和的輸入訊號；這種詮釋很有價值，因為它允許使用熟悉的波德圖 (Bode diagram) 來確定這些系統的穩定度裕量 (stability margins) 和穩態響應 (steady-state response)。

圖 2. 連續時間控制演算法回授迴路中的延遲元件滿足了週期性輸入的內部模型原理，但實際上包含大量（理論上無限多個）振盪器，以複製任意週期性輸入。
 

諧波消除 (Harmonic Cancellation)

作為重複控制的特例，諧波消除針對特定離散頻率進行擾動抑制，考慮將重複控制應用於有限數量的離散頻率的特殊情況，即諧波消除；這些情況在精密運動控制應用中很常見，包括：

• 力與轉矩漣波 (Force and torque ripple)
• 旋轉軸上的不平衡負載 (Unbalanced payloads)
• 週期性命令輪廓 (Cyclic command profiles)
• 螺桿導程與齒輪節距 (Screw lead and gear pitch)
• 鏈條式電纜支撐系統 (Link-style cable carrier systems)

請注意，某些擾動可能是時間上的週期性，而其他擾動則是在位移上具有週期性，因此特定頻率可能會變化；讓我們假設有一個系統在恆定速度下運行，且具有已知頻率；以「外掛式」風格實作諧波消除演算法，可以根據需要輕鬆啟用和停用（圖 3 中的代表性方塊圖包含了諧波消除演算法、標準 PID 控制器以及受控體 (plant)）；為符合內部模型原理，諧波消除演算法包含平行的振盪器 (parallel oscillators)，擾動訊號中包含的每個頻率都有一個對應的振盪器；藉由觀察單一頻率擾動的情況，可以注意到諧波消除演算法在頻域中的效果，演算法中的每個獨立振盪器都有一個連續時間的拉普拉斯轉換表示：

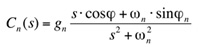
圖 4 展示了當增益項 K 從零（停用振盪器）掃描至較高值時，諧波消除演算法的頻率響應圖，注意：在振盪器頻率 (ω) 處的增益幅度 (magnitude) 為無限大；現在，回想一下熟悉的積分器項如何為恆定擾動提供零穩態誤差；簡言之，我們可以將諧波消除區塊簡單地詮釋為一個在非零頻率下的積分器；由擾動引起的追蹤誤差在振盪器頻率處恆為零，我們可以透過回顧圖 3 的方塊圖，並計算出由擾動 D(s) 引起的追蹤誤差 E(s) 來驗證這一點：
 

在此表示式中評估振盪器頻率 ω：

在感興趣的頻率點上，對於擾動存在零穩態誤差；當目標是追蹤週期性輪廓時，類似的分析顯示在命令輪廓與實際位置輪廓之間具有單位響應 (unity response) 且相位移為零 (zero phase shift)；總之，控制演算法中的振盪器對於特定振盪器頻率的訊號，作用如同一個「積分器」項；平行應用多個振盪器可以消除更複雜的波形，並趨近於全功能重複控制器的一般情況，這些演算法是以「外掛式」控制器的形式實現，使得標準 PID 控制增益保持不變；當應用諧波消除演算法時，我們使用熟悉的頻域調整工具來確定穩定度裕量（交越頻率 (crossover frequency)、相位裕量 (phase margin) 和增益裕量 (gain margin)）；然而，一般而言，由於諧波消除演算法作用最活躍的頻率範圍非常有限，只要校正頻率遠低於系統的交越頻率，這些系統的調整就相對直接；圖 5 展示了一個啟用了諧波消除演算法之系統的實際開迴路頻率響應 (open-loop frequency response)；在系統交越頻率以下的迴路增益中，顯著的峰值非常突出；然而，它們的影響足夠局部化，因此在交越頻率處的增益和相位相對不受影響。

圖 3. 諧波消除演算法 C(s) 以「外掛式 (plug-in)」架構實現。這使得 PID 控制器保持不變，並允許隨時啟用和停用諧波消除演算法。

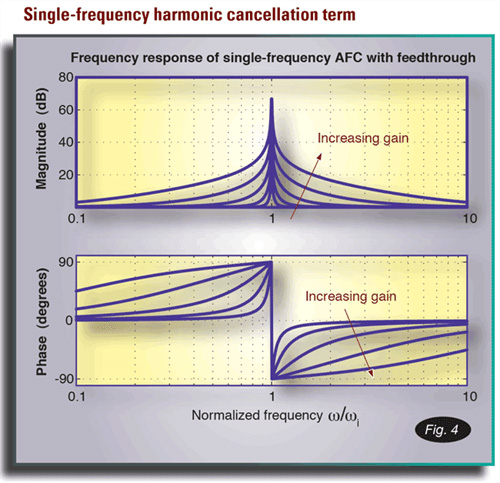
圖 4. 波德圖顯示在振盪器頻率處具有非常高（無限大）的增益幅度。

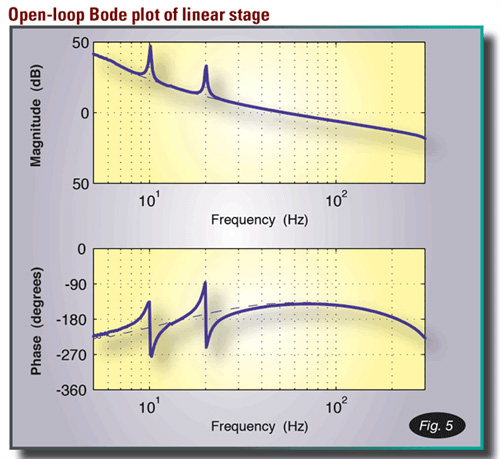
圖 5. 迴路增益在 10 Hz 和 20 Hz 的消除頻率處急劇增加。即便如此，它們對接近 55 Hz 交越頻率處的響應影響甚微。

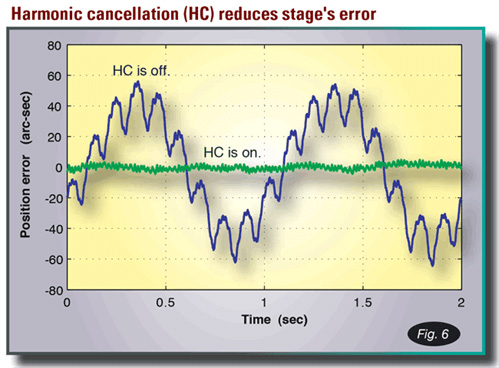
圖 6. 將諧波消除演算法應用於水平安裝的旋轉平台，在 60 rpm 轉速下，將均方根追蹤誤差減少約 12 倍。在此繪製的案例中，主要誤差來源是負載不平衡以及馬達極週期上的轉矩變化。

應用範例

諧波消除的實用價值展現在多種精密應用中，一旦理解了內部模型原理、重複控制和諧波消除的整體概念，它們便能廣泛應用於各種情境，特別是在要求高精度的航空航太與國防系統中：
 

• 範例 1： 考量磁碟機讀寫臂的控制，這些磁碟並非繞著完美的真實軸線旋轉，但將重複控制應用於誤差運動的同步部分，可以改善讀寫頭追蹤運動的能力；類似的精密追蹤需求也存在於光電追蹤系統或資料記錄儀器中。
   
• 範例 2： 用於非對稱車削操作的快速刀具伺服機構 (Fast tool servomechanisms) 也受益於重複控制，當車削環面形狀（例如用於矯正散光的隱形眼鏡模具）的表面時，切削刀具基本上隨著主軸的每次旋轉回到相同的位置；這種週期性的刀具路徑可以分解為其傅立葉級數係數，並對每個係數應用諧波消除振盪器；類似的週期性運動補償在精密光學製造或天線剖面加工中亦有關鍵作用。
   
• 範例 3： 一個直接的應用是具有水平安裝旋轉平台的系統，例如雷達基座或感測器指向儀；在某個特定案例中，設計者需要改善此類機器的速度穩定性，每轉一次的不平衡量以及每轉九次的馬達極節距是主要的擾動項（參見圖 6，顯示平台以 60 rpm 旋轉時量測到的位置誤差）；在這些頻率應用諧波消除演算法，將均方根 (RMS) 追蹤誤差從 33 角秒 (arc-sec) 減少到 1.7 角秒，減少了約 12 倍；這種精度提升對於目標追蹤或穩定平台至關重要。

圖 7. Motion Simulator 軟體可匯入並產生運動輪廓，並允許 I/O 監控與控制（上圖）– 此外還有頻率響應模式（左圖），用於詳細的運動評估。

Aerotech：滿足您獨特的運動控制需求

特定製程運動控制解決方案

• 高精度的雷射加工 (如 LaserTurn 系列平台)
• 微米級的光纖對準與光子元件測試 (如 FiberMaxHP, FiberAlign, FiberGlide 系列)
• 精密的表面形貌量測 (如 SMP 平台)
• 或是要求氣密性的雷射封裝焊接 (如 HermeSys 系統)

客製化運動平台解決方案

• 多軸整合與特殊運動軌跡 (如 XY-Theta 系統、六軸/七軸/八軸複合運動系統)
• 空氣軸承、機械軸承或混合軸承的靈活選用與配置 (如各式客製化 IGM 系統、分軸空氣軸承系統、平面空氣軸承系統)
• 特殊環境對應 (如真空、潔淨室) 或特殊負載/尺寸需求 (如高負載平衡旋轉台、大行程龍門系統、重載平面空氣軸承系統)
• 針對特定儀器或製程設備的精密整合 (如多軸薄層成像系統)

從桌上型 XYZ 運動系統到大型模組化龍門系統，Aerotech 的客製化運動平台不僅滿足您的規格要求，更在精度、動態性能與長期可靠性上達到業界頂尖水準。
| 了解更多 >
 

關於作者

Stephen Ludwick 博士，機電整合研究總監
Stephen Ludwick 在 Aerotech 擔任永續工程總監，負責開發用於系統特性分析與控制的工具；他在精密運動控制領域擁有超過二十五年的經驗，持有卡內基美隆大學和麻省理工學院的機械工程學位，並在匹茲堡大學擔任兼任教員。